Simon Boyé, Gael Guennebaud et Pascal Barla présenteront lors du SIGGRAPH Asia 2012 leur travail de recherche A Vectorial Solver for Free-form Vector Gradient, qui permet d’améliorer la création de dégradés complexes en dessin vectoriel. Le Gradient Mesh (filet de dégradé) désormais présent dans des logiciels comme Illustrator permet en effet d’aller plus loin que le simple dégradé linéaire, mais pose des problèmes pratiques lors de son utilisation. Nous les avons interrogés pour en savoir plus sur leur publication, qui pourrait doter les artistes de meilleurs outils créatifs, que ce soit pour la création d’images vectorielles à la main, la réalisation d’effets 2,5D ou pour la vectorisation d’images.
Voici la vidéo de présentation :
3DVF : Bonjour Simon, Pascal et Gaël. Vous allez présenter la publication A Vectorial Solver for Free-form Vector Gradients au SIGGRAPH Asia 2012. Quel était l’objectif de ce travail de recherche ?
Simon Boyé, Pascal Barla, Gael Guennebaud : Bonjour ! Ce projet s’inscrit dans le cadre du dessin vectoriel, plus particulièrement de la création de dégradés de couleur complexes. La plupart des infographistes sont familiers avec les outils de base tels que les dégradés linéaires ou radiaux que l’on peut trouver dans des applications comme Illustrator ou Inkscape. Depuis quelques années, l’outil filet de dégradé (Gradient Mesh en Anglais) a fait son apparition, et permet la création de dégradés de couleur complexes à partir d’un maillage et de couleurs associées aux points de contrôle. L’inconvénient majeur de cette méthode est que la création de dégradés de plus en plus complexes demande un maillage de plus en plus dense, alors que l’approche dessin se veut par essence fondée sur des tracés de forme libre.
L’objectif de notre projet était donc de proposer de nouveaux outils de dessin vectoriel, qui préservent cette liberté d’utilisation, tout en permettant aux infographistes de produire des dégradés d’une complexité arbitraire. Concrètement, l’artiste va placer des courbes et des points qui vont diffuser des couleurs dans l’image, jusqu’à ce que « les couleurs rencontrent » d’autres courbes ou points de contrôle.
3DVF : La méthode est une extension d’une publication présentée en 2008 lors du SIGGRAPH, « Diffusion Curves » (Pascal était d’ailleurs l’un des auteurs). Quelles limites de cette technique vous ont poussé à aller plus loin ?
S.B., P.B., G.G. : La méthode originale propose déjà cette idée de diffuser des couleurs de part et d’autre de courbes de contrôle, mais possède deux limitations principales.
Tout d’abord, la méthode s’appuie sur l’équation de Laplace, qui caractérise la propagation de la chaleur dans un milieu ; sauf que dans le cas de dégradés vectoriels, ce sont les couleurs qui sont propagées dans l’image. Ce choix a pour avantage de pouvoir propager des couleurs partout dans l’image quelle que soit la configuration des courbes de contrôle; et pour inconvénient de ne proposer qu’un contrôle indirect sur la propagation à proprement parler. Cette limitation a été en partie corrigée par des extensions proposées dans des articles qui ont suivi, notamment par l’utilisation d’une interpolation bi-harmonique qui permet à la fois de produire des dégradés plus naturels, et un contrôle de type « tangentes » (qui influe sur la vitesse de propagation des couleurs). Dans les deux cas, une modification en un point de l’image peut influencer potentiellement tout autre point de l’image ce qui n’est pas toujours souhaitable.
De plus, la totalité de ces méthodes, Diffusion Curves originales incluses, produisent un résultat à une résolution donnée ; elles doivent être complètement recalculées dès lors qu’une simple transformation (zoom, rotation) est appliquée. Cela les rend inutilisables en pratique sans l’exploitation de cartes graphiques dernier cri, et même dans ces cas là, la résolution finale reste limitée, tout comme les possibilités d’édition et d’animation. Ce n’est pas le cas des Gradient Meshes car celles-ci sont directement représentées sous la forme de primitives vectorielles élémentaires, qui sont facilement affichables et imprimables à une résolution arbitraire.
3DVF : En quelques mots, pouvez-vous nous décrire la méthode proposée ?
S.B., P.B., G.G. : L’idée principale de notre méthode est simple: convertir les courbes/points de contrôle et le résultat de la propagation de couleur dans un maillage dynamique, caché à l’utilisateur. En quelque sorte, notre approche consiste à créer une structure similaire au Gradient Mesh automatiquement, tandis que l’utilisateur manipule courbes et points de contrôle de manière totalement libre. Ceci explique le titre que nous avons choisi : la méthode est « free-form » de par son utilisation, mais produit toujours un résultat « vectoriel » sous la forme d’une triangulation.
Sur le plan technique, l’approche est organisée en 2 étapes:
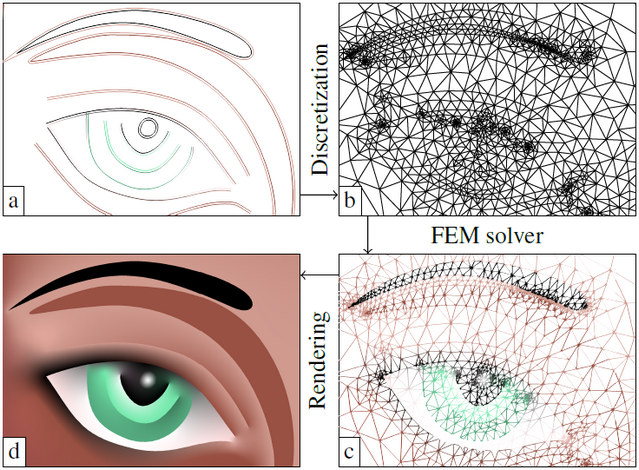
1) L’algorithme crée d’abord un maillage triangulaire qui passe exactement par les courbes/points de contrôle et qui possède une densité de triangle adaptée à la complexité du dessin. Ce type d’approche est employé dans d’autres domaines comme la sculpture digitale (ex : l’outil dynamesh dans ZBrush).
2) L’équation bi-harmonique est résolue sur ces triangles, ainsi assignant un dégradé vectoriel élémentaire à chacun d’entre eux, en s’appuyant sur une méthode d’éléments finis. Ce type d’outil mathématique est souvent utilisé pour modéliser des déformations en mécanique.
Chacun des triangles ainsi générés est ensuite facilement affichable par tout système de dessin vectoriel, sans pour autant nécessiter de carte graphique avancée.
Ci-dessus, aperçu de la méthode employée : les primitives vectorielles (a) servent à créer le maillage (b), et la résolution permet de lui assigner un dégradé vectoriel (c). On peut ensuite rendre l’image (d).
3DVF : Quelles sont ses points forts et ses applications possibles ?
S.B., P.B., G.G. : En premier lieu, la méthode produit en sortie un maillage facile à évaluer (en temps réel), quelle que soit la résolution d’affichage ou d’impression, alors que l’utilisateur de la méthode manipule des courbes et des points sans se soucier de leur emplacement. La solution s’inscrit donc parfaitement dans la boite à outils de dessin vectoriel, tout en permettant une bien plus vaste variété de compositions de couleurs. Nous montrons quelques exemples qui vont du dessin réaliste au stylisé dans l’article et la vidéo correspondante.
Ci-dessus, un des résultats obtenus : la technique utilisée étant indépendante de la résolution, on peut zoomer à loisir dans l’image.
En plus de cela, le maillage résultant peut être mis à profit de différentes manières. Tout d’abord, faire un zoom ou une rotation de l’image revient simplement à appliquer ces opérations sur le maillage. De plus, la méthode permet de créer différentes instances d’un même maillage pour peupler l’images de nombreux dessins complexes ; nous donnons un exemple de forêt éditée en temps réel dans nos résultats. De la même manière, le maillage pourrait être déformé via de multiples outils, comme par exemple en utilisant une déformation perspective, toujours en temps réel. Dans l’article nous montrons également comment effectuer la propagation des couleurs à la surface d’un objet 3D. Il est important de comprendre qu’aucune de ces opérations ne serait réalisable de manière efficace à partir des Diffusion Curves originales ou de leurs extensions.
Enfin, nous avons étendu la gamme des contrôles possibles en proposant de nouveaux types de courbes, en particulier les courbes dites de « transmission ». Celles-ci permettent de localement bloquer la propagation des couleurs dans un seul sens tandis qu’elles sont transmises dans l’autre. Elles fournissent ainsi un contrôle local qui manquait fortement dans les méthodes précédentes.
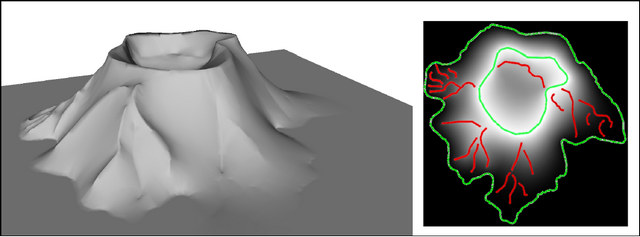
Parmi les applications possibles, il y a bien sûr la création de dégradés de couleur, mais nous avons aussi montré comment créer des champs de hauteur (pour la création de terrains 3D), voire même comment créer des images de normales vectorielles, qui peuvent à leur tour être utilisées pour déformer des images d’environnements vectoriels (donnant ainsi l’illusion d’une surface miroir courbée). C’est un type d’application qui nous intéresse beaucoup ces temps-ci : comment donner l’illusion du shading avec des outils exclusivement 2D, ici vectoriels.
Ci-dessus, une normal map créée à partir de zéro est utilisée pour déformer des images et créer une illusion d’objet réfléchissant. Ci-dessous, une height map est générée avec quelques courbes (en rouge et vert) et permet de créer facilement un terrain 3D.
3DVF : Inversement, sur quels points est-elle limitée ?
S.B., P.B., G.G. : Dans son état actuel, notre programme n’est pas très facile à manipuler : il existe de nombreux types de courbes utilisables, et il faut expérimenter avec plusieurs choix pour trouver lequel est le bon pour accomplir un dégradé de couleurs donné. C’est avant tout un problème d’ingénierie et d’interface, mais un problème toutefois intéressant : comment regrouper les possibilités de notre approche sous la forme de presets (des outils) qui restent intuitifs dans leur utilisation ? Ce genre de question n’est pas abordé lors de la phase de recherche dans notre domaine, mais se révèle être cruciale pour que la méthode soit adoptée par les utilisateurs.
Une autre limitation de la méthode est sa performance lors de l’édition des courbes/points, qui dépend du nombre de primitives de contrôle présentes dans l’image. C’est encore une fois un problème d’ingénierie important sur lequel nous ne nous sommes pas penchés, mais pour lequel de nombreuses solutions sont envisageables : méthodes de culling, de fast preview, voire de résolution progressive, etc.
3DVF : Quel a été l’implication des différents auteurs de la publication ?
S.B., P.B., G.G. : Ce travail s’inscrit avant tout dans les travaux de thèse de Simon Boyé, qui avait auparavant travaillé sur les surfaces de subdivision. Il a travaillé avec Gaël Guennebaud, son encadrant, sur le coeur technique du problème, à savoir la mise au point des méthodes de triangulation et d’éléments finis. Pascal Barla a rejoint le groupe pour aider à situer et comparer la méthode aux travaux précédents (dont il était l’un des auteurs), puis pour exploiter la solution dans diverses applications allant au delà des dégradés de couleur.
3DVF : Les applications sont évidemment intéressantes dans le secteur du dessin vectoriel, mais la publication évoque aussi, dans sa conclusion, d’éventuelles application en vectorisation d’images. Pouvez-vous nous en dire plus ?
C’est un problème assez complexe à priori. Il existe des méthodes qui convertissent une image sous la forme d’un maillage avec dégradés de couleur, mais le résultat est difficilement éditable car chaque sommet du maillage (souvent extrêmement dense) doit être manipulé par l’utilisateur. Nous envisageons une solution différente : tout d’abord extraire les discontinuités dans l’image (nos courbes de contrôle) ; ensuite construire une triangulation en fonction de ces courbes ; et enfin trouver le type des courbes et les couleurs à leur associer en fonction du contenu de chaque triangle.
C’est ce que l’on appelle un « problème inverse ». Si elle se révélait concluante, on se retrouverait à l’issue de cette conversion avec une image tout autant éditable que si elle avait été créée à la main. En particulier, le maillage serait à nouveau mis a jour dynamiquement durant l’édition. En plus d’être malléable à souhait, une telle approche serait aussi nettement plus compacte, et pourrait notamment servir pour représenter des light maps (qui sont caractérisées par des dégradés lisses et de fortes discontinuités).
3DVF : Allez-vous poursuivre dans cette voie ?
S.B., P.B., G.G. : Pas dans l’immédiat. Nous sommes pour le moment plus intéressé dans l’exploration des capacités 3D de la méthode, ainsi qu’aux possibilités de shading 2.5D qu’apportent de tels outils de dessin. Pour poursuivre ces recherches, nous aurons probablement besoin d’étudiants (niveau master) et/ou d’ingénieur(s). N’hésitez pas à nous contacter si c’est un sujet qui vous passionne !
Pour plus de détails :
La page de la publication permet de la télécharger en pdf et propose quelques visuels, dont ceux utilisés pour illustrer cet article.
Site des auteurs : Simon Boyé, Pascal Barla et Gael Guennebaud.
A noter enfin, nous avions proposé sur 3DVF une interview sur la publication Surface Flows for Image-Based Shading Design à l’occasion du SIGGRAPH 2012, à laquelle Pascal Barla avait participé.